三余弦定理

引入

在做有些数学题时，总是会遇到这种类似的题：

如右图，点O是正方形纸片ABCD的中心，点E，F分别为AD，BC的中点，现沿对角线AC把纸片折成直二面角，则纸片折后∠EOF的大小为？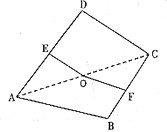

不难想象，当OE和OF变化时，∠EOF也在变化。可以说，在二面角不变的情况下，∠EOF是由OE和OF与二面角的交线的夹角确定的

因为OE和OF与二面角的交线的夹角是一定的，所以∠EOF自然是确定的，所以肯定是能算出来的。

因此，会让人想到，有没有一个公式可以直接套用，直接算出来∠EOF的角度。

三余弦定理

这里引入一个模型，如图

模型

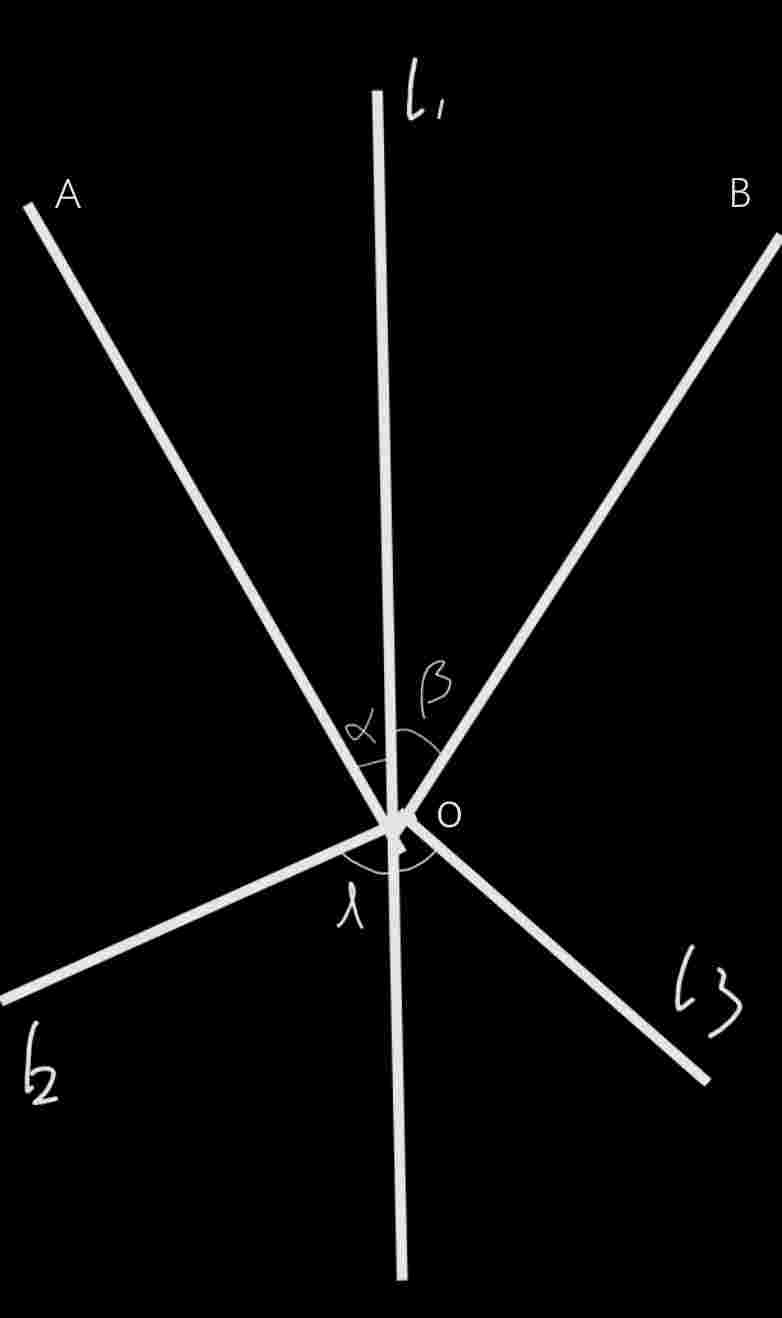
l1和l2在一个面内，记为平面M，l1和l3在另一个面内，记为平面N。l1，l2，l3交于O，l1⊥l2，l1⊥l3，λ为l2和l3的夹角，所以为二面角。射线OA在M中，射线OB在N中。OA与l1的夹角记为α，OB与l1的夹角记为β。OA与OB的夹角记为θ，求θ。

结论：cosθ=cosαcosβ+sinαsinβcosλ

至于怎么推的，以后再说。（提示：勾股定理+余弦定理就可以推出来）

应用

对于上面那道题，α=135º，β=45º，λ=90º，带入公式可得θ=120º